- Research
- Open access
- Published:
Attribute-based data retrieval with semantic keyword search for e-health cloud
Journal of Cloud Computing volume 4, Article number: 10 (2015)
Abstract
Data retrieval on encrypted documents is a very important technology in cloud storage, where encryption on sensitive data is a necessary operation to protect documents privacy before they are outsourced to cloud. Most of existing searchable encryption schemes concentrate on single-user scenario. In this paper, we focus on the multiple sender and multiple user application scenario to provide a flexible search authorization searchable encryption (SE) scheme. The attribute based encryption (ABE) technology is used to support fine-grained access control and the synonym keyword search is enabled in the new scheme. The new primitive is named as attribute based searchable encryption with synonym keyword search function (SK-ABSE). The formally definition of SK-ABSE is given together with a concrete construction. This scheme also enables convenient user revocation mechanism.
Introduction
With the fast development of cloud computing, more and more users turns to new computing paradigm for convenient accessing to a shared pool of resources. It brings about ubiquitous and flexible access, on-demand computing resource configuration and vast computation resources at a very low price. Despite of these convenience, it also has potential risks when data owner loses directly control over their information. Privacy concern becomes the main obstacle that hiders the adoption of cloud storage by corporations.
Data encryption is a straightforward way to protect security and privacy. However, traditional encryption methods will prevent the commonly used query operation on confidential data. The keyword search becomes difficult when data are encrypted. In 2004, Boneh et al. [1] proposed the first public key encryption scheme with keyword search (PEKS) to deal with the issue of searching on confidential data. Since then, many efforts are made to improve the efficiency [2-4], enhance the security [5-7] or provide new flexible properties [8-12].
Although these schemes provide new features to search on encrypted data, they can not realize flexible and fine-grained access control on outsourced data. Sahai et al. [13] proposed the concept of attribute-based encryption (ABE) in Eurocrypt 2005, which extends the notion of identity based encryption (IBE). ABE schemes [14-18] enable flexible access policy on secret data and makes data sharing quite easy. In ABE scheme, each user has a set of attributes. An access policy is defined to determine that the users with certain attributes are authorized to access the shared data.
In this paper, we propose a new primitive named as attribute-based searchable encryption scheme with semantic keyword search function (SK-ABSE). The main contributions are listed as following.
-
–
No Secret Key Sharing. A certain set of attributes is associate with user, which is also embedded in user’s private key. It avoids the risk that brought by secret key sharing in multiple user. When a data sender outsources the sensitive data to cloud server, he specifies an access policy in the data encryption phase and generate a secure index for extracted keyword. Only if the set of attributes of user satisfies the access structure in encrypted data, the user is permitted to query on those information.
-
–
Semantic Keyword Search. A novel point is that semantic keyword search is enabled in this scheme. It means all documents that contain synonym related keywords will be returned when the user query on a keyword. A concrete construction of SK-ABSE is proposed, which is built on bilinear pairings.
-
–
Fine-grained Search Authorization. It supports multiple data sender and multiple data user. Fine-grained search authorization is enabled, which is enforced by data owner.
-
–
User Revocation. User revocation can be efficiently processed and is suitable for e-health cloud application. It also ensures the privacy of queries and secrecy of data contents.
The rest of the paper is organized as follows. Section Preliminaries reviews some preliminary notions. Section Definitions for SK-ABSE Scheme defines the SK-ABSE and a system model is given. Section A SK-ABSE Construction presents the SK-ABSE constructions and analyzes the security. Section Conclusions concludes this paper.
Preliminaries
Bilinear map
Let G and G 1 be two (multiplicative) cyclic groups of prime order p. Let g be a generator of G. Bilinear map e is a map e:G×G→G 1 with the following properties:
-
1.
Bilinearity: e(u a,v b)=e(u,v)ab, for all u,v∈G,a,b∈Z p ;
-
2.
Non-degeneracy: \(e(g,g)\neq 1_{G_{1}}\) ;
-
3.
Computability: there exists an efficient algorithm to calculate e(u,v), for all u,v∈G.
WordNet
In traditional English dictionaries, vocabulary entries are always organized according the alphabetical order and the synonymous relationship between vocabularies is totally ignored. WordNet [19] is a lexical database for English language, which combines modern computer technology and the research result of Cognitive Psycholinguistics research. It was created in the Cognitive Science Laboratory of Princeton University under the direction of psychology professor George Armitage Miller starting in 1985 and has been directed in recent years by Christiane Fellbaum.
Unlike traditional dictionaries, WordNet groups English words into sets of synonyms which is called "synsets". It provides short definitions and usage examples and records a number of relations among the synonym sets or their members. WordNet can thus be seen as a combination of dictionary and thesaurus. It is accessible to human users via a web browser. The database and software tools are also freely available for download from the WordNet website [19]. WordNet includes the lexical categories nouns, verbs, adjectives and adverbs but ignores prepositions, determiners and other function words. In our scheme, WordNet is used to extend a keyword into its "synsets" in order to fulfill the semantically keyword search.
For a keyword w, it will be extended to a synonym set {w,s 1,⋯,s n } through using WordNet, in which s 1,⋯,s n are the synonyms of keyword w. Then, this synonym set ("synset" for short) will be re-ordered according to the lexicographical order and denoted as Γ w .
Access structure
Access structure is used to describe the policy of access control. It defines the concepts of authorized access subset and unauthorized access subset. It works quite similar to secret sharing. Some set of participants is able to reconstruct the shared secret while other sets can not.
Let \(\mathcal {P}=\{P_{1},P_{2},\cdots,P_{l}\},l\in Z^{+}\) be a set of participants. The shared secret is denoted as s. A set of participants that is capable to reconstruct s is named as authorized subset. While others are called unauthorized subsets. A set that consists of all authorized subsets is denoted as Γ. At the meanwhile, a set that consists of all unauthorized subsets is denoted as \(\overline {\Gamma }=2^{\mathcal {P}}\setminus \Gamma \).
An access tree is usually used to represent the the access structure (i.e., access policy). Let  be an access tree and each internal node (i.e., not leaf node) be a threshold gate. Let n
u
m
x
be the number of children of node x and k
x
be the threshold value of x with 1≤k
x
≤n
u
m
x
. If k
x
=n
u
m
x
, the logic gate of node x is "
A
N
D
", which means that the shared secret can be recovered if and only if all attributes are satisfied. If k
x
=1, the logic gate of node x is "
O
R
", which means that the shared secret can be recovered when one of the attributes is satisfied. Each leaf node l in access tree
be an access tree and each internal node (i.e., not leaf node) be a threshold gate. Let n
u
m
x
be the number of children of node x and k
x
be the threshold value of x with 1≤k
x
≤n
u
m
x
. If k
x
=n
u
m
x
, the logic gate of node x is "
A
N
D
", which means that the shared secret can be recovered if and only if all attributes are satisfied. If k
x
=1, the logic gate of node x is "
O
R
", which means that the shared secret can be recovered when one of the attributes is satisfied. Each leaf node l in access tree  is associated with an attribute a
t
t
r
l
. The parent node of l in access tree
is associated with an attribute a
t
t
r
l
. The parent node of l in access tree  is represented as p
a
r
a
n
t(l). All child nodes of parent node x are labeled by a number i
n
d
e
x(x) between 1 and n
u
m
x
.
is represented as p
a
r
a
n
t(l). All child nodes of parent node x are labeled by a number i
n
d
e
x(x) between 1 and n
u
m
x
.
Let \(\mathcal {T}_{x}\) with a root node x be the subtree of access tree  . If an attribute set Ψ satisfies the access policy of \(\mathcal {T}_{x}\), we denote it as \(\mathcal {T}_{x}(\Psi)=1\). Otherwise, \(\mathcal {T}_{x}(\Psi)=0\). The following recursion algorithm is used to calculate whether an attribute set Ψ satisfies the access policy of \(\mathcal {T}_{x}\).
. If an attribute set Ψ satisfies the access policy of \(\mathcal {T}_{x}\), we denote it as \(\mathcal {T}_{x}(\Psi)=1\). Otherwise, \(\mathcal {T}_{x}(\Psi)=0\). The following recursion algorithm is used to calculate whether an attribute set Ψ satisfies the access policy of \(\mathcal {T}_{x}\).
-
If x is not a leaf node, this algorithm will calculate the value of \(\mathcal {T}_{x'}(\Psi)\) for each child node x ′ of x. It returns 1 if and only if at least there are k x values of \(\mathcal {T}_{x'}(\Psi)\) equal to 1. Otherwise, it returns 0.
-
if x is a leaf node, this algorithm will return 1 if and only if a t t r x ∈Ψ. Otherwise, it returns 0.
Definitions for SK-ABSE scheme
An e-health cloud storage system for multiple users is considered to enable flexible access control and data retrieval on encrypted electronic health record (EHR). The system model that involves four entities is shown in Figure 1. Key distribution center (KDC) is responsible for key distribution. Cloud storage center (CSC) is a honest but curious data center, who provides information storage and data retrieval service. The data sender (DS) uploads encrypted EHR data to cloud server for confidential data storage. Data user (DU) is a cloud subscriber with a set of attributes to describe his identity.
The system works as follows. KDC is a fully trusted third party by all entities in the system. KDC firstly generates system global parameters and distribute attribute related private keys to users. DS is responsible to generate encrypted files and extract keyword to create secure index, which are outsourced to CSC. Distinct access policy will be sent for different document before uploading. The outsourced health records can be shared with authorized users. CSC is deemed as semi-trusted, who is not only honest follow the operations specified by the scheme, but also strive to filch as much as possible information from encrypted EHR content and data retrieval request. DU could execute keyword query on encrypted EHR files. If the DU has attributes that satisfies the access policy defined by the data sender for encrypted documents, DU is capable to operate the data retrieval of those files. DU is able to generate trapdoor for keyword search and decrypt EHR files. KDC also has the authority to add or revoke the access right of participants. A revocation list of user will be provided to cloud center.
In our system, the user set is denoted as \(\mathcal {U}=\{U_{1},U_{2},\cdots,U_{l}\}\) and the attribute set as Φ={φ
1,φ
2,⋯,φ
n
}. Ψ
i
is used to identify the attribute set of user U
i
.  is the access policy on ciphertext.
is the access policy on ciphertext.
A SK-ABSE scheme consists of the following polynomial-time algorithms.
-
–
Setup. The setup algorithm is run by KDC, which takes as input a security parameter k. It outputs a global parameter GP and the master secret key MSK for the system. The GP is made public and MSK is kept secret. It is described as S e t u p(k)→(G P,M S K).
-
–
KeyGen. The key generation algorithm is also executed by KDC. The public input to the algorithm consists of the system global parameter GP, the user’s identity U i and an attribute set Ψ i of user U i . The private input to KDC is the system master secret key MSK. The output of this algorithm is the public key \(pk_{U_{i}}\phantom {\dot {i}\!}\) and private key \(sk_{U_{i}}\phantom {\dot {i}\!}\) of user U i . The private key \(sk_{U_{i}}\phantom {\dot {i}\!}\) is confidentially sent to user U i . This algorithm is described as \(KeyGen(GP,MSK,U_{i},\Psi _{i}) \to (pk_{U_{i}}, sk_{U_{i}})\phantom {\dot {i}\!}\).
-
–
Encrypt. The encryption algorithm is run by data sender. Taken as input the system global parameter GP,a message M, the public key \(pk_{U_{i}}\) of user U i , a keyword w and an access structure
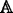 , it will extend the keyword w to its synonym set and then encrypt it to a ciphertext CT and a secure index I
w
. The \((CT,I_{w},\mathbb {A})\)-tuple is outsourced to cloud. This algorithm is described as \(Encrypt(GP,pk_{U_{i}},M,w,\mathbb {A}) \to (CT,I_{w})\).
, it will extend the keyword w to its synonym set and then encrypt it to a ciphertext CT and a secure index I
w
. The \((CT,I_{w},\mathbb {A})\)-tuple is outsourced to cloud. This algorithm is described as \(Encrypt(GP,pk_{U_{i}},M,w,\mathbb {A}) \to (CT,I_{w})\). -
–
Trapdoor. The keyword trapdoor generation algorithm is run by data user. On input the system global parameter GP, a keyword w and the private key \(sk_{U_{i}}\phantom {\dot {i}\!}\) of user U i , this algorithm outputs a trapdoor T w for keyword w. This algorithm is described as \(Trapdoor(GP,sk_{U_{i}},w)\to T_{w}\).
-
–
Retrieve. The data retrieval algorithm is run by CSC. Taken as input the system global parameter GP, the keyword secure index I w , the trapdoor T w corresponding to keyword w, the attribute set Ψ i of user U i and the access structure
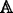 , this algorithm will output 1 if Ψ
i
satisfies
, this algorithm will output 1 if Ψ
i
satisfies  and the trapdoor T
w
matches I
w
. This algorithm is described as Retrieve
\((GP,I_{w},T_{w},{\Psi _{i}},\mathbb {A}) \to 1\;or\;0\).
and the trapdoor T
w
matches I
w
. This algorithm is described as Retrieve
\((GP,I_{w},T_{w},{\Psi _{i}},\mathbb {A}) \to 1\;or\;0\). -
–
Decrypt. The decryption algorithm is operated by data user. Taken as input the system global parameter GP, the ciphertext CT, the attribute set Ψ i of user U i , the access structure
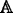 and the private key \(sk_{U_{i}}\phantom {\dot {i}\!}\) of user U
i
, this algorithm will output the plaintext M if the attribute set Ψ
i
of user U
i
satisfies the access structure
and the private key \(sk_{U_{i}}\phantom {\dot {i}\!}\) of user U
i
, this algorithm will output the plaintext M if the attribute set Ψ
i
of user U
i
satisfies the access structure 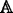 associated with the ciphertext CT. This algorithm is described as \(Decrypt(GP,CT,sk_{U_{i}},\Psi _{i},\mathbb {A})\to M\).
associated with the ciphertext CT. This algorithm is described as \(Decrypt(GP,CT,sk_{U_{i}},\Psi _{i},\mathbb {A})\to M\).
Security Requirements In this system, the confidentiality of data should be guaranteed. Since EHR files and the indexes are outsourced to cloud, they can be easily analyzed by CSC and the adversary. The security of the scheme should ensure that both of them can not obtain the secret data in those outsourced files. Moreover, the privacy of keyword query must be protected. The extracted keyword are usually the core information of the EHR files. The keyword query can be eavesdropped by attackers and cryptographic analyzed by CSC. The keyword trapdoor should be secure enough to resist those attacks. In this multiple user system, undeniable of request should be satisfied. No adversary is able to construct a legible keyword trapdoor and the authorized user can not denial his request.
A SK-ABSE construction
Construction
Let Φ={φ 1,φ 2,⋯,φ n } be the attribute set of users. A hash function H is denoted as: \(H:\;\{0,1\}^{*}\to Z_{p}^{*}\phantom {\dot {i}\!}\). The proposed attribute-based searchable encryption scheme with semantic keyword search (SK-ABSE) is described as follows.
-
S e t u p(k)→(G P,M S K).
On input a secret parameter k, KDC randomly chooses a generator g of group G with order p. Random elements α,t 1,t 2,⋯,t n are selected from \(Z_{p}^{*}\phantom {\dot {i}\!}\). KDC computes y=e(g,g)α and \(T_{i}=g^{t_{i}}\phantom {\dot {i}\!}\). KDC publishes system global parameter as G P=(g,y,T i ) and keeps secret the master secret key M S K=(α,t i ) for 1≤i≤n.
-
\(KeyGen(GP,MSK,U_{i},\Psi _{i}) \to (pk_{U_{i}},sk_{U_{i}})\phantom {\dot {i}\!}\).
This algorithm takes as input the global parameter GP, the system master secret key MSK and the attribute set Ψ i for user U i . To generate private key for user U i , the following steps will be executed by KDC.
-
Select random r,η from \(Z_{p}^{*}\phantom {\dot {i}\!}\).
-
Compute \(d_{0}=g^{\alpha -r},d_{0}'=\eta,pk_{U_{i}}=g^{\eta }\phantom {\dot {i}\!}\).
-
For each attribute ψ j in set Ψ i , KDC computes \(d_{j}=g^{r\cdot t_{j}^{-1}}\).
-
The public key \(pk_{U_{i}}\) of user U i is published in the system.
-
The secret key \(sk_{U_{i}}=(d_{0},d_{0}',d_{j}|\;\forall \;\psi _{j}\in \Psi _{i}))\) is confidentially sent to user U i .
-
\(Encrypt(GP,pk_{U_{i}},M,w,\mathbb {A}) \to (CT,I_{w})\).
This algorithm takes as input a system global parameter GP, the public key \(pk_{U_{i}}\) of user U
i
, a plaintext M, a keyword w and the corresponding access structure  . To create confidential ciphertext CT and secure keyword index I
w
, the following steps are executed by data sender.
. To create confidential ciphertext CT and secure keyword index I
w
, the following steps are executed by data sender.
-
–
Choose a random \(s\in Z_{p}^{*}\) and compute C 0=g s,C 1=M·y s.
-
–
Let the access tree corresponding to access structure
 to be
to be  . The root of access tree
. The root of access tree  is denoted as R with a value s.
is denoted as R with a value s.The following distribution is made according to the “AND” or “OR” relationship between parent node and child node.
∘ If the relationship of parent node and child node is “OR”, the value of child node is set to s.
∘ If the relationship of parent node and child node is “AND” and there exists t child node, DS chooses random numbers \(s_{1},s_{2},\cdots,s_{t-1}\in Z_{p}^{*}\) and compute \(s_{t}=s-\sum _{i=1}^{t-1}s_{i}\). Then, DS assigns these values to t child nodes.
-
–
For each node \(\varphi _{j,i}\in \mathcal {T}\), compute \(C_{j,i}=T_{j}^{s_{i}}\phantom {\dot {i}\!}\).
-
–
The synonym set Γ w of keyword w is constructed by using WordNet. Note that the words in Γ w is ranked in lexicographical order.
-
–
Select random \(\tau \in Z_{p}^{*}\phantom {\dot {i}\!}\) and compute \(A=g^{\tau }, B=e(g^{H(\Gamma _{w})},(pk_{U_{i}})^{\tau })\phantom {\dot {i}\!}\).
-
–
The ciphertext of message M is \(CT=(\mathcal {T},C_{0},C_{1},C_{j,i}|\psi _{j,i}\in \mathcal {T})\). The secure index of keyword w is I w =(A,B).
-
–
DS outputs the ciphertext CT together with the secure index I w and access structure
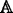 to cloud server for sharing.
to cloud server for sharing.
-
\(Trapdoor(GP,sk_{U_{i}},w)\to T_{w}\).
In order to generate a trapdoor for keyword w, data user firstly choose a random \(\lambda \in Z_{p}^{*}\). Extend the keyword w to its synonym set Γ w through utilizing WordNet. Output keyword trapdoor T w =(T w,1,T w,2)=(λ,H(Γ w )·λ·d0′).
-
\(Retrieve(GP,I_{w},T_{w},{\Psi _{i}},\mathbb {A}) \to 1\;or\;0\).
To operate data retrieval, an interaction between DU and CSC is executed as following.
-
–
DU initialize a keyword retrieval request by sending to CSC a trapdoor T w for the keyword w and an attribute set Ψ i related to user U i ’s private key \(sk_{U_{i}}\phantom {\dot {i}\!}\).
-
–
CSC searches \((CT,I_{w},\mathbb {A})\) in the user U i ’s cloud storage to find secure index I w with the designated keyword w. CSC should verify whether the attribute Ψ i satisfies access structure
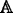 associated with I
w
.
associated with I
w
. -
–
CSC tests whether the equation holds for I w =(A,B) and T w =(T w,1,T w,2):
$$e(A,g^{T_{w,2}})=B^{T_{w,1}}. $$If the equation holds and Ψ i satisfies
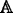 , CSC outputs 1. Otherwise, it outputs 0.
, CSC outputs 1. Otherwise, it outputs 0. -
–
All matched ciphertext set \({\mathcal {CT}}=\{CT_{1},CT_{2},\cdots \}\) will be sent to DU.
-
\(Decrypt(GP,CT,sk_{U_{i}},\Psi _{i},\mathbb {A})\to M\).
After receiving the matched ciphertext set \({\mathcal {CT}}\), DU uses his private key \(sk_{U_{i}}\phantom {\dot {i}\!}\) to decrypt the ciphertext as following.
-
–
Choose the minimum set Ψ i′∈Ψ i that could satisfy access structure
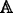 .
. -
–
Recover the message M by computing:
$$C_{1}/[e(C_{0},d_{0})\cdot\prod_{\varphi\in\Psi_{i}}e(C_{j,i},d_{j})]=M.$$
-
Access Right Revocation.
If the access right of user U i expires or a revocation of U i ’s access right is executed before its expiration, the following operations will be executed.
-
Generate a revocation certificate as \(Revoke_{U_{i}}=\{U_{i},Date,Sig_{\textit {MSK}}(U_{i},Date)\}\), which consists of the user name U i , the revocation data Date and signature on these information generated by using master secret key MSK.
-
KDC sends the revocation certificate to CSC for storage.
-
CSC adds the certificate to revocation list. A data retrieval request will be rejected if the user is found in revocation list.
Security analysis
Proposition 1.
The proposed SK-ABSE scheme is correct.
Proof.
The correctness of keyword query is proved as follows.
Thus, we have \(e(A,g^{T_{w,2}})=B^{T_{w,1}}\phantom {\dot {i}\!}\).
The correctness of decryption can be verified as follows.
-
Confidentiality of Data.
In the proposed scheme, plaintext documents are encrypted to ciphertext controlled by access policy before they are outsourced to CSC. Both CSC and adversary can not get the private information in those ciphertext.
The keyword is extracted by data sender in local terminal and encrypted by user’s public key to a secure index \(I_{w}=(A,B)=(g^{\tau },e(g^{H(\Gamma _{w})},(pk_{U_{i}})^{\tau }))\phantom {\dot {i}\!}\). The index can not be disclosed if the private key of user is kept secret. The random \(\tau \in Z_{p}^{*}\) is introduced to resist replay attack from adversary.
-
Privacy of Query.
In the keyword query phase, user’s private key is used to protect the synonym set Γ w and the keyword trapdoor is generated T w =(T w,1,T w,2)=(λ,H(Γ w )·λ·d0′). When CSC receives the request, it can not deduce Γ w from the trapdoor and the privacy of query can be ensured. The random element \(\lambda \in Z_{p}^{*}\) is used to prevent adversary from replay attacks. Attacker can not eavesdrop the trapdoor information and retransmit it to CSC for illegal query.
-
Undeniable of Request.
This system supports queries from multiple users. In traditional multi-user system, a secret key is shared by multiple users. For a query request, both CDC and KDC could distinguish the request generated by one user from another. Therefore, non-repudiation of query request is supported. However, in the multi-user system designed in this paper, each user is distributed different private keys, so that the submitted query request T W contains the information of user’s private key. Any adversary or CSC can not forge the trapdoor information generated by authorized user. At the meanwhile, the user can not denied their request. Therefore the query request phase satisfies undeniability.
Conclusions
Searchable encryption is a new technology that can simultaneously provide encryption and ciphertext retrieval function. To solve the problems in existing multiple user SE schemes, a novel SE scheme is designed to support fine-grained access control policy and semantic keyword search. A concrete construction is provided based on bilinear pairing. Security analysis shows that the scheme could guarantee the privacy of data and keywords, and has the advantage of non-repudiation.
Abbreviations
- ABE:
-
Attribute based encryption
- IBE:
-
Identity based encryption
- SK-ABSE:
-
Attribute based searchable encryption with synonym keyword search
- PEKS:
-
Public key encryption scheme with keyword search
- SE:
-
Searchable encryption
- EHR:
-
Electronic health record
- KDC:
-
Key distribution center
- CSC:
-
Cloud storage center
- DS:
-
Data sender
- DU:
-
Data user
References
Boneh D, Di Crescenzo G, Ostrovsky R, Persiano G (2004) Public Key Encryption with Keyword Search In: EUROCRYPT, 506–522.. Springer, Heidelberg.
Gu C, Zhu Y, Zhang Y (2007) Efficient public key encryption with keyword search schemes from pairings In: INSCRYPT, 372–83.. Springer, Heidelberg.
Long B, Gu D, Ding N, Lu H (2012) On Improving the Performance of Public Key Encryption with Keyword Search In: CSC, 143–147.. IEEE, Piscataway, N.J, USA.
Chen Z, Wu C, Wang D, Li S (2012) Conjunctive keywords searchable encryption with efficient pairing, constant ciphertext and short trapdoor In: PAISI, 176–189.. Springer, Heidelberg.
Xu P, Jin H, Wu Q, Wang W (2013) Public-Key Encryption with Fuzzy Keyword Search-A Provably Secure Scheme under Keyword Gusssing Attack In: IEEE Transactions on Computers, 2266–2277.. IEEE, Piscataway, N.J, USA.
Wang B, Yu S, Lou W, Hou T (2014) Privacy-Preserving Multi-Keyword Fuzzy Search over Encrypted Data in the Cloud In: INFOCOM’14, 2112–2120.. IEEE, Piscataway, N.J, USA.
Cao N, Wang C, Li M, Ren K, Lou W (2014) Privacy-preserving multi-keyword ranked search over encrypted cloud data In: IEEE Transactions on Parallel and Distributed Systems, 222–233.. IEEE, Piscataway, N.J, USA.
Attrapadung N, Furukawa J, Imai H (2006) Forward-Secure and Searchable Broadcast Encryption with Short Ciphertexts and Private Keys In: ASIACRYPT 2006, LNCS 4284, 161–177.. Springer, Heidelberg.
Bosch C, Brinkman R, Hartel P, Jonker W (2011) Conjunctive wildcard search over encrypted data In: International Conference on Secure Data Management, LNCS 6933, 114–127.. Springer, Heidelberg.
Li J, Wang Q, Wang C, Cao N, Ren K, Lou W (2010) Fuzzy keyword search over encrypted data in cloud computing In: Proceedings of the 29th IEEE International Conference on Computer Communications(INFOCOM10), 441–445.. IEEE, Piscataway, N.J, USA.
Hu C, He P, Liu P (2012) Public Key Encryption with Multi-keyword Search In: NCIS2012, 568–576.. Springer, Heidelberg.
Hwang M, Hsu S, Lee C (2014) A New Public Key Encryption with Conjunctive Field Keyword Search Scheme In: Information Technology and Control, 277–288.. Kaunas Univ. Technology, Kaunas, Lithuania.
Sahai A, Waters B (2005) Fuzzy Identity Based Encryption In: EUROCRYPT’05, LNCS 3494, 457–473.. Springer, Heidelberg.
Waters B (2011) Ciphertext-Policy Attribute-Based Encryption: An Expressive, Efficient, and Provably Secure Realization In: PKC’11, LNCS 6571, 53–70.. Springer, Heidelberg.
Wang C, Luo J (2013) An Efficient Key-Policy Attribute-Based Encryption Scheme with Constant Ciphertext Length. Mathematical Problems in Engineering. volume 2013, Article ID 810969, http://dx.doi.org/10.1155/2013/810969.
Qin B, Deng H, Wu Q, Domingo-Ferrer J, Naccache D, Zhou Y (2015) Flexible attribute-based encryption applicable to secure e-healthcare records. International Journal of Information Security, vol. 14, nol. 1, Springer, Heidelberg, pp 1–13.
Hohenberger S, Waters B (2014) Online/offline attribute-based encryption In: PKC’14, 293–310.. Springer, Heidelberg.
Han J, Susilo W, Mu Y, Zhou J, Au MH (2014) PPDCP-ABE: Privacy-Preserving Decentralized Ciphertext-Policy Attribute-Based Encryption In: ESORICS’14, 73–90.. Springer, Heidelberg.
WordNet Documentation. http://wordnet.princeton.edu/wordnet/documentation/.
Acknowledgements
This research is supported by National Natural Science Foundation of China (61402112, 61472307, 61472309).
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
The contribution of this work is summarized as following. A new primitive is proposed named as attribute-based searchable encryption with semantic keyword search (SK-ABSE). It supports multiple data sender and multiple data user. Fine-grained search authorization is enabled, which is enforced by data owner. Semantic keyword search is supported in this scheme. It means all documents that contain synonym related keywords will be returned when the user query on a keyword. User revocation can be efficiently processed. It also ensures the privacy of queries and secrecy of data contents.
Authors’ information
Yang Yang is a lecture in the College of Mathematics and Computer Science at Fuzhou University. She received the Ph.D degree from Xidian University in 2011. Her research interests are in the area of information security and privacy protection.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits use, duplication, adaptation, distribution, and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Yang, Y. Attribute-based data retrieval with semantic keyword search for e-health cloud. J Cloud Comp 4, 10 (2015). https://doi.org/10.1186/s13677-015-0034-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13677-015-0034-8

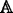 , it will extend the keyword w to its synonym set and then encrypt it to a ciphertext CT and a secure index I
w
. The
, it will extend the keyword w to its synonym set and then encrypt it to a ciphertext CT and a secure index I
w
. The 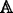 , this algorithm will output 1 if Ψ
i
satisfies
, this algorithm will output 1 if Ψ
i
satisfies  and the trapdoor T
w
matches I
w
. This algorithm is described as Retrieve
and the trapdoor T
w
matches I
w
. This algorithm is described as Retrieve
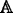 and the private key
and the private key 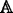 associated with the ciphertext CT. This algorithm is described as
associated with the ciphertext CT. This algorithm is described as  to be
to be  . The root of access tree
. The root of access tree  is denoted as R with a value s.
is denoted as R with a value s.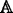 to cloud server for sharing.
to cloud server for sharing.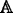 associated with I
w
.
associated with I
w
.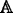 , CSC outputs 1. Otherwise, it outputs 0.
, CSC outputs 1. Otherwise, it outputs 0.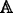 .
.