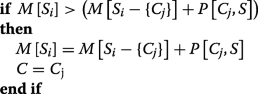Pricing strategies of an oligopolist in federated cloud markets

Abstract

In this paper, we study how an oligopolist influences the coalition structure in federated cloud markets. Specifically, we use cooperative game theory to model the circumstances under which a cloud provider prefers to join a cloud federation vis-a-vis consider taking a price offer made by an oligopolist. We consider two price offering strategies for an oligopolist: non-adaptive and adaptive. In non-adaptive strategy, an oligopolist makes a price offer to all the cloud providers simultaneously. It can be noted that the oligopolist can buy-out all the cloud providers by making a price offer which is equal to a core allocation and the total price offer made by the oligopolist is equal to the value of the grand coalition. In adaptive strategy, the oligopolist approaches the cloud providers one after another in a sequential manner. We show that by using the adaptive strategy, the oligopolist can buy-out all the cloud providers at a total price offer which is less than that of the non-adaptive strategy.

Introduction

The current cloud computing market structure is akin to oligopoly as few mega cloud providers completely own the market share. Each of them individually or in collusion has the power to affect the market prices leading to what is called an imperfect competition. Further, due to the large scale of operations in the data centers owned by these oligopolists, there is an acute stress on electricity and other natural resources. Many studies [1, 2] indicated the resulting adverse impact on the environment due to carbon emissions and other pollutants.

Since computing has become a common commodity these days, it is easy to envisage a large number of micro cloud providers with small to medium scale data centers. With the presence of a large number of producers, an oligopolistic market leans towards a perfectly competitive market. In a market with perfect competition, producers become price takers and it is not possible for one or few cloud providers to affect the market prices. Further, as these small data centers are geographically spread out, the stress on the local resources and the impact on the micro-climate will be mitigated, especially by the usage of renewable energy resources and productive use of dissipated heat energy.

However, such micro cloud providers will be able to serve only moderate sized consumer requests due to the limited availability of resources in their data centers. In order to serve large consumer requests many micro cloud providers have to come together and form a coalition or a federation. The federation formation can happen in a peer-to-peer fashion leading to what is called a Peer-to-Peer Inter-Cloud Federation (refer Fig. 1a) [3]. The other option is to use the services of a broker as in Fig. 1b resulting in a Multi-Cloud federation model. The broker is one of the very few oligopolists who owns a substantial market share. He can generate more revenue and thereby profit, using the same set of resources when compared with micro cloud providers. This is due to his market reach, brand value and other value-added services he can provide.

Fig. 1

Cloud Federation Models

Problem statement and contributions

In this section, we briefly outline the problems addressed in this paper and the later sections provide a detailed technical discussion regarding the same ¹.

Peer-to-peer inter-clouds and linear production games

Given a set of cloud providers, we formulate the problem of peer-to-peer inter-cloud federation formation (refer Fig. 1a) as a linear production game. This is the first contribution of this paper. It is a well-known theorem that every linear production game has a non-empty core [5, 6]. A core is a pay-off distribution scheme such that no individual player or a sub-coalition of players have an incentive to break-off from the grand coalition. For many cooperative game theoretic models, there are no known polynomial time algorithms for computing a core allocation. However, for linear production games, computing a core involves solving the dual of a linear programming problem, which can be done computationally efficiently.

Intervention of an oligopolist

An oligopolist may intervene in the formation of a peer-to-peer cloud federation and pursue individual cloud providers to subscribe to the services of a broker, in this case the oligopolist himself, resulting in the Multi-Cloud model (refer Fig. 1b). When an oligopolist makes a price offer to each of the cloud providers, some may take up the offer and others may not. This results in the grand coalition splitting up into sub-coalitions. We say that a sub-coalition is feasible if each member cloud provider gets a greater pay-off than that offered by the oligopolist. A collection of such feasible sub-coalitions forms what we call a stable coalition structure. The notion of a stable coalition structure has hitherto not been considered in research literature. Further, given a price offer vector from an oligopolist, we propose an efficient algorithm for the computation of a stable coalition structure. These ideas constitute the second main contribution of the current paper.

Oligopolist price determination

Thirdly, we study the price offering strategies which an oligopolist can use to induce the cloud providers to lend their resources to him while maximizing his profit. The simplest price determination strategy for an oligopolist is to compute the core and make a price offer which is the same as that of a core. This non-adaptive strategy gives a lower bound on the profit an oligopolist can make. However, an oligopolist can approach the cloud providers with price offers one after another in a strategic manner. We call this as an adaptive price offering strategy. In this paper, we show that adaptive price offering strategies can yield more profit to an oligopolist when compared with non-adaptive strategies. To the best of our knowledge, the problem statements in Intervention of an oligopolist and Oligopolist price determination section are completely novel and no prior related work exists.

In Background section, we provide the necessary background on cooperative game theory and linear production games; in Federation formation and payoff distribution using linear production games section, we formulate the cloud federation formation and payoff distribution problems using linear production games; in Intervention of an oligopolist in federation formation section, we show the impact of an oligopolist on federation formation and how we can arrive at stable coalition structures; related experimental analysis is provided in Experimental analysis section; in Oligopolist price determination section, we present non-adaptive and adaptive price offering strategies of an oligopolist; Related work section contains the related work; and finally we conclude with Conclusions section.

Background

In this paper, we model the proposed problem as a linear production game, a class of games from the cooperative game theory [5, 6]. Towards this end, we provide a brief overview of cooperative game theory concepts, which will be used in the rest of the paper.

Cooperative game theory

Given a set of N={1,⋯,n} players, a subset S⊆N of them can pool their resources and form a coalition to generate an utility or value v(S). We say that the utility is transferable if it can be split among the members of the coalition in an arbitrary fashion.

Definition 1

A cooperative n-person game in coalitional form is denoted by G=(N,v) where $v: 2^{N} \rightarrow {\mathbb R}^{+}$, with v(ϕ)=0. The function v is called the characteristic function of the game and v(S) is called the value of the coalition S.

A cooperative game G=(N,v) can induce a subgame G_S=(S,v_S) where S⊆N and v_S(T)=v(T) for all T⊆S. We say that a cooperative game is super-additive if v(S∪T)≥v(S)+v(T) for all S,T∈2^N with S∩T=ϕ. Clearly, when a game is super-additive, then players find it beneficial to form coalitions of larger size. However, the formation of a grand coalition N or any other coalition depends on the payoff vectors allocated to the players.

Definition 2

A payoff vector $x=(x_{1},\cdots,x_{n})\in {\mathbb R}^{n}$ is called an imputation if it satisfies the following individual rationality and efficiency conditions.

• 1 Individual rationality: x_i≥v({i}) ∀i∈N.

• 2 Efficiency: $\sum _{i=1}^{n} x_{i} = v(N)$.

The set of imputations associated with a game G=(N,v) is denoted by I(G). For a payoff vector x and a coalition S⊆N, let x(S) denote $\sum _{i\in S} x_{i}$.

Definition 3

The core of a game G=(N,v) denoted as C(G) is defined as follows.

$$ \begin{aligned} C(G) = \{~x \in I(G)~|~x(F) \geq v(F)~\forall F\subseteq N~\}. \end{aligned} $$

If the payoff vector is from the core, then there is no incentive for any sub-coalition S⊂N to deviate from the grand coalition N, thus ensuring stability. However, the core of a game is not necessarily non-empty. Bondareva [7] and Shapley [8] gave independently a characterization of games with a non-empty core.

Definition 4

A map $\lambda : 2^{N} \setminus \{\phi \} \rightarrow {\mathbb R}^{+}$ is called a balanced map if

$$ \begin{aligned} \sum_{S\in 2^{N} \setminus \{\phi \}} \lambda(S)e^{S} = e^{N},\\ \end{aligned} $$

where for a coalition S⊆N the vector $e^{S}\in \mathbb R^{n}$ is defined as $e_{i}^{S}=1$ if i∈ S and $e_{i}^{S} =0$ if i∈N∖S.

Definition 5

A cooperative game G=(N,v)is called a balanced game if for each balanced map $\lambda : 2^{N} \setminus \{\phi \} \rightarrow {\mathbb R}^{+}$ the following condition holds good.

$$ \begin{aligned} \sum_{S\in 2^{N} \setminus \{\phi \}} \lambda(S)v(S) \leq v(N). \end{aligned} $$

Further, a cooperative game G=(N,v) is called totally balanced if every induced subgame G_S=(S,v_S) for all S∈2^N∖{ϕ} is balanced.

The following theorem due to Bondareva and Shapley characterizes the set of games with a non-empty core.

Theorem 1

A cooperative game G=(N,v) will have a non-empty core if and only if it is a balanced game.

Linear production games

Consider a production situation where m different types of products P₁,…,P_m can be manufactured using q distinct kind of resources G₁,…,G_q. Further, there is a production matrix A_m×q whose (j,k)^th entry a_jk denotes the number of units of resource G_k required to manufacture an unit of product P_j. Overall, the j^th row of the matrix denoted by a_j gives the overall resource requirements per unit of product P_j. The linearity of the production situation comes from the fact that to manufacture α units of product P_j the corresponding resource requirements scale-up linearly to αa_j. Let the j^th entry of the price vector c_1×m=(c₁,⋯,c_m) denote the price per unit of product P_j. Given a resource bundle b_q×1=(β₁,⋯,β_q)^T with non-negative entries, the optimal production plan x_m×1=(x₁,⋯,x_m)^T is obtained by solving the following linear programming problem.

$$ \begin{aligned} &\underset{x}{\text{Maximize}}\,\,\, c \cdot x \\ &\text{subject to}\,\, A^{T} \cdot x \leq b\\ & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\hspace*{5ex}x \geq 0 \end{aligned} $$

Consider now an n-player game G=(N,v) wherein the resource bundle owned by the i^th player is denoted by b_i. The resource bundle owned by a coalition S⊆N is defined as $b(S) = \sum _{i\in S} b_{i}$. Since each b_i is a resource vector, the summation denotes the usual vector addition operation. The value v(S) associated with the coalition S is obtained by solving the following linear programming problem.

$$ \begin{aligned} & \underset{x}{\text{Maximize}} \,\,\,c \cdot x \\ & \text{subject to} \,\,A^{T} \cdot x \leq b(S)\\ & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\hspace*{5ex}x \geq 0 \end{aligned} $$

The following is an important theorem which we use in this paper.

Theorem 2

Every linear production game G_lp=(N,v) is totally balanced. Hence not only the core C(G_lp) is non-empty but also the core C(G_S) of every induced subgame G_S=(S,v_S) where S⊆N is also non-empty.

The algorithmic idea behind computing a core allocation from C(G_S) is to first formulate the dual problem for the primal problem posed above. The solution to the dual problem gives the shadow prices for the q distinct resources used while manufacturing m distinct products in various quantities so as to maximize revenue. We can then derive the pay-offs to the individual players based on their resource contribution and the shadow prices computed from the dual problem.

Federation formation and payoff distribution using linear production games

In this section, we will present a model for peer-to-peer inter-cloud federation and an efficient payoff distribution scheme which gives a core allocation using linear production games.

Federation formation model

Let ${\mathcal {I}}=\{{C}_{1},\cdots,{C}_{n}\}$ be a collection of cloud providers. A cloud provider C_i owns a resource bundle $b_{i} = (b^{c}_{i}, b^{m}_{i}, b^{s}_{i})^{T}$ where $b_{i}^{c}$ is the total number of available compute cores; $b_{i}^{m}$ and $b_{i}^{s}$ denotes the total available main memory and secondary storage respectively. The cloud providers can offer m types of virtual machines denoted by VM_j,1≤j≤m. The core, main memory and storage requirements for each virtual machine type is given by the production matrix A_m×3 whose j^th row, $a_{j} = (a_{j}^{c}, a_{j}^{m}, a_{j}^{s})$, corresponds to the resource configuration vector of a virtual machine of type VM_j. Table 2 gives example virtual machine types and the associated production matrix used in the experimental analysis section of this paper. The per unit market price of different types of virtual machines is denoted by the price vector p=(p₁,⋯,p_m). Table 2 also provides the hourly rental price for various types of virtual machines considered. Given this market scenario, the cloud providers have to decide upon a federation structure such that each of them maximize their respective payoffs.

It can be observed that we can model this problem by constructing a linear production game which is exactly similar to the game G = (N,v) described in the Linear production games section. We denote the total pooled cores, memory and storage from a federation S by b^c(S),b^m(S) and b^s(S) respectively. The value v(S) associated with a federation S is obtained by solving the following linear programming problem OPTLP(S).

$$\begin{array}{*{20}l} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \underset{x}{\text{Maximize}} & \quad \sum_{j=1}^{m} x_{j} p_{j} \end{array} $$

(1a)

$$\begin{array}{*{20}l} \text{subject to} & \quad \sum_{j=1}^{m} x_{j} a^{c}_{j} \leq b^{c}(S) \end{array} $$

(1b)

$$\begin{array}{*{20}l} & \quad \sum_{j=1}^{m} x_{j} a^{m}_{j} \leq b^{m}(S) \end{array} $$

(1c)

$$\begin{array}{*{20}l} & \quad \sum_{j=1}^{m} x_{j} a^{s}_{j} \leq b^{s}(S) \end{array} $$

(1d)

$$\begin{array}{*{20}l} & \quad x_{j} \geq 0 ~(1 \leq j \leq m) \end{array} $$

(1e)

Constraints 1b, 1c and 1d denote the capacity constraints corresponding to core, memory and storage respectively. In fact, this game being super additive, we can infer that the grand coalition generates the maximum revenue, which is obtained by solving the linear programming problem OPTLP(N). Further, from Theorem 2, we know that there is a core allocation possible as it is a totally balanced game. In the next section, we show how we can do payoff distribution using a core allocation, thereby achieving the stability of the grand coalition.

Payoff distribution

Owen [9] showed that we can compute a core allocation for a linear production game G_lp=(N,v) by solving the following dual problem associated with the primal problem OPTLP(N).

$$\begin{array}{*{20}l} {}\underset{y}{\text{Minimize}} & \quad y_{1} b^{c}(N) + y_{2} b^{m}(N) + y_{3} b^{s}(N) \end{array} $$

(2a)

$$\begin{array}{*{20}l} {}\text{subject to} & \quad y_{1} a^{c}_{j} \,+\, y_{2} a^{m}_{j} \,+\, y_{3} a^{s}_{j} \geq p_{j} ~(\forall j, 1\leq j \leq m) \end{array} $$

(2b)

$$\begin{array}{*{20}l} & \quad y \geq 0 \end{array} $$

(2c)

We interpret the optimal solution $y_{*}=(y_{*}^{c}, y_{*}^{m}, y_{*}^{s})$ to the dual problem as the shadow prices for cores, memory and storage. Owen proved that we can obtain a core allocation vector by paying the i^th player with the resource bundle $b_{i}=(b^{c}_{i}, b^{m}_{i}, b^{s}_{i})^{T}$ as follows.

$$ \begin{aligned} \alpha_{i}(N) = \sum_{j\in \{c, m, s\}} y_{*}^{j} b_{i}^{j} \end{aligned} $$

We denote the payoff vector as α(N)=(α₁(N),⋯,α_n(N)) where the parameter N indicates that the payoff corresponds to the grand coalition. The subset of core allocations which are formed using optimal dual solutions is know as the Owen set. In Intervention of an oligopolist in federation formation section, we will present how a broker or an oligopolist can intervene in the formation of a grand coalition by offering higher payoff to individual cloud providers.

Discussion

The idea of carving out virtual machines of different types by aggregating the cores, memory and storage from different cloud providers is used in prior work [10, 11]. In practice, it is impractical to construct a virtual machine with cores from one cloud provider and memory from another, for example. In fact, even within the same premises of a cloud provider, it is not possible to have a virtual machine with cores from one physical machine and memory from another. So a virtual machine has to be carved out using the resources available on a single physical machine. However, at the data center level, resources within a physical machine are usually proportionate. It means that a physical machine with large number of cores usually has large memory and storage capacity. In fact, the storage could be network attached and not associated with the physical machine directly. From this, we can intuitively infer that the optimal virtual machine production plan $(x_{1}^{*},\cdots,x_{m}^{*})$ obtained from solving the OPTLP(S) problem can be almost realized while respecting the practical physical constraints. There could be some small number of remnant virtual machines which cannot be realized but the impact on the optimality of the solution will be minimal. Another approach to handle remnant virtual machines is by using a small reserve pool of physical machines at every micro data centre. Overall, we argue that the linear programming formulation is a reasonable approximation to estimate the value of a coalition as it is not only computationally efficient but also lends itself to the computation and analysis of pay-off distribution schemes through the framework of linear production games. We validate this intuitive argument through experimental analysis in Optimality of linear production games formulation section.

Intervention of an oligopolist in federation formation

In order to maintain market control, the oligopolists may intervene in the peer-to-peer federation formation, refer Fig. 1a, by offering incentives to the micro cloud providers to lend their resources to them. The oligopolists in turn use the lent resources to supply virtual machines to the end consumers potentially at a higher price due to their wider market reach. During this process, an oligopolist assumes the role of a broker leading to a multi-cloud architecture depicted in Fig. 1b. In the rest of this section, we study how an oligopolist can affect the structure of cloud federation and the resulting impact on the payoff to individual cloud providers.

Let an oligopolist offers a price m_i to rent the entire resource bundle b_i from the cloud provider C_i. In this paper, we study the restricted problem of an interaction between a single oligopolist and a set of cloud providers². One simple way of considering more than one oligopolist is to set the price offer m_i made to the cloud provider C_i to the maximum of the offers made by different oligopolists in the market, and the rest of the theory proposed in this section holds good.

Core allocation for subgames

In Payoff distribution section, we described how the payoff distribution vector α(N) can be computed for the game G_lp=(N,v). Since, every subgame G_S=(S,v_S) induced by G_lp is also a linear production game, we can analogously compute the payoff distribution vector α(S) by solving the dual problem for the primal problem OPTLP(S). Overall, we have to solve 2ⁿ−1 linear programming problems to compute the payoff distribution vectors for all the induced subgames, which is computationally expensive. However, it can be noted from the constraints (2b) and (2c), the feasible region for the dual problem of OPTLP(S) is independent of the federation S and only the coefficients of the objective function change. Hence, for practical values of m, we can enumerate the basic feasible solutions, in other words, the extreme points of the polyhedra defined by the dual problem constraints. For different objective functions associated with different subgames, we can exhaustively check the list of extreme points and find the optimal solution.

Influence of the oligopolist

Definition 6

The marginal payoff for a cloud provider C_i with respect to a coalition S and a price offer m_i from an oligopolist is defined as

$$ \begin{aligned} \beta_{i}(S) = \alpha_{i}(S) - m_{i}. \end{aligned} $$

A cloud provider has an incentive to deviate from a federation S and take up the offer of an oligopolist if and only if β_i(S)<0. Thus the oligopolist may destabilize the grand coalition as all the cloud providers whose β_i(N)<0 will break away from the coalition.

Definition 7

For a cooperative game G=(N,v) and a price offer vector m=(m₁,⋯,m_n), a coalition S⊆N is called a feasible coalition if and only if β_i(S)≥0 for all i∈S.

From the discussion in Core allocation for subgames section, we can enumerate the list of all feasible coalitions in 2^N by computing the respective payoff distribution vectors.

Definition 8

Given price offer vector m, we call a partition CS={F₁,⋯,F_k−1,F^∗} of the player set N as a stable coalition structure if

• 1 The coalitions F_i,1≤i≤k−1 are feasible coalitions.

• 2 There exists no subset S⊆F^∗ which is a feasible coalition. Thus all the cloud players from F^∗ take the price offer made by the monopolist.

Note that if m_i<v({i}), then cloud provider C_i is a feasible coalition by himself.

Finding a stable coalition structure

There can be many possible stable coalition structures for a given price offer vector from the oligopolist. We may prefer one stable coalition structure to other based on certain criteria. For example, one criteria could be to minimize the number of cloud providers taking up oligopolist’s offer, i.e., |F^∗|. Another criteria could be to be maximize the sum of payoffs of all the cloud providers, i.e., $\sum _{i=1}^{k-1} \sum _{j \in F_{i}} \alpha _{j}(F_{i}) + \sum _{j \in F^{*}} m_{j}$.

Definition 9

For a feasible coalition F and a price offer vector m=(m₁,⋯,m_n), we associate a goodness value g(F) which is defined as follows.

$$ \begin{aligned} g(F) = \sum_{i\in F} (\alpha_{i}(F) - m_{i})/|F| \end{aligned} $$

In this paper, we propose the following simple greedy algorithm for stable coalition formation.

• 1 Let the initial coalition structure be CS=ϕ. Repeat the following step until it terminates.

• 2 (i^th iteration)

  • (a) Among all the feasible coalitions, choose a coalition F_i with a maximum goodness value g(F_i) and F∩F_i=ϕ for all F∈CS.

  • (b) If there exists no feasible coalition which is disjoint with the already chosen feasible coalitions, then exit the algorithm after setting F^∗=N−∪_F∈CSF and CS=CS∪{F^∗}.

The time complexity of the above algorithm is dominated by the computation of the payoff values α_i(F), for 1≤i≤n and F⊆N. This involves solving 2ⁿ linear optimization problems. Further, we can easily note from the above algorithm, that different goodness functions will yield different coalition structures. In the next section, we do an experimental analysis on the influence of an oligopolist on stable coalition formation and overall payoff distribution.

Experimental analysis

In this section, we study how increasing price offers from an oligopolist to the individual cloud providers impact the structure of stable coalitions formed. We consider a set of 12 cloud providers $\mathcal {I}=\{C_{1},\cdots, C_{12}\}$ whose resource capacities are given in Table 1. These resource capacities are randomly chosen, first by choosing one of the three buckets: small, medium and large; and then choosing a capacity randomly within a range determined by that bucket type. Inspired from Microsoft Azure, we let each cloud provider offer four types of virtual machines: General Purpose (B2S), Storage Optimized (L4), Memory Optimized (E8 v3), and Compute Optimized (F16 v2). The resource requirements of each type of virtual machine is given in Table 2. The same table also provides the hourly rental price for each type of virtual machine.

Table 1 Resource capacity of cloud providers. vCPUs are expressed in 100s of cores, memory and storage in 100 GB units

Table 2 VM instance types, their resource configurations and hourly rental prices

We consider l=45 different market scenarios. In the i^th market scenario, M_i,1≤i≤l, the oligopolist makes a price offer m=(m₁,⋯,m_j,⋯,m₁₂) wherein

$$ \begin{aligned} m_{j} = \left(1+\frac{i}{100}\right) \times v\left(\left\{C_{j}\right\}\right). \end{aligned} $$

(3)

That means the oligopolist is offering a price which is i% greater than the value a cloud provider can generate by working all alone. For small values of i, a cloud provider can potentially get better payoff by forming a coalition; whereas for larger values of i he may be better off taking up the oligopolist’s offer. This can be observed from the Fig. 2 which depicts how the stable coalition structure evolves with the increasing price offers from the oligopolist. The stable coalition structures are computed using the greedy algorithm proposed in Finding a stable coalition structure section. Each track of the semi-circle represents the coalition structure for a given price offer. The yellow colored cloud providers are those who take up the oligopolists offer. Similar colored cloud providers in a track belong to the same coalition. For example, at one percent price offer, the coalition structure is CS={{1,2,5,11},{3,6},{4,10},{8,9},{7,12}}. The members of the last set F^∗={7,12} are those who accepted the offer made by the oligopolist. Further, the semi-circle shows only those tracks where there is a change in the coalition structure from the previous market scenario. For example, since the coalition structure did not change from the market scenario M₇ till M₁₇, the intervening coalition structures are not represented. We can notice the increasing yellow color as we move from inside to outside in the semi-circle indicating that with increasing price offers more cloud providers will lean towards the oligopolist. This is further illustrated by the graph in Fig. 3a which shows the size of F^∗,|F^∗|, with increasing price offers. Another interesting observation is that a cloud provider may take an oligopolist’s offer in market scenario M_i but may change his mind in $\phantom {\dot {i}\!}M_{i^{\prime }}$ where i^′>i. This is due to the overall change in the coalition structure. This phenomenon can be observed by looking at the sector corresponding to the cloud provider 5 in Fig. 2.

Fig. 2

Evolution of coalition structure with increasing price offers going from market scenario M₁ to M₄₅ (refer Eq. 3)

Fig. 3

Analysis of different market scenarios

Figure 3b shows the average marginal payoff of the cloud providers who preferred to form a peer-to-peer coalition. For a given market scenario, if CS is a stable coalition structure (refer Definition 8), then the average marginal payoff is defined as $\phantom {\dot {i}\!}\sum _{F_{i} \in CS\setminus F^{*}}\sum _{j\in F_{i}} \beta _{j}(F_{i})/|N\setminus F^{*}|$. As expected, with the increasing price offer from the oligopolist, the marginal payoff goes down. However, it needs not be monotonic, as it may increase locally due to the changes in the stable coalition structure. Figure 4a shows the total time taken for the computation of the stable coalition structure for a given market scenario. It can be noted that overall it is in the order of milliseconds and hence computationally feasible problem to solve for all practical purposes. Further, with increasing price offers, the number of feasible coalitions go down, which makes the greedy algorithm converge faster.

Fig. 4

Left panel depicts time taken to compute stable coalition structure. Right panel compares the payoff from the coalition and the oligopolist in the first market scenario

For a coalition, we know that v_S(S) is the total payoff available for the coalition S. The combined payoff from an oligopolist to a coalition S is $\sum _{i\in S} m_{i}$. Figure 4b compares the coalitional payoff and the combined broker payoff for all the coalitions in the market scenario M₁. For cloud providers 7 and 12, who take up the oligopolist’s offer, these two values are almost the same (one percent difference).

Optimality of linear production games formulation

In Discussion section, we discussed the shortcomings of the linear production games and why despite that, it is still a reasonable market model to adopt. The primary issue in linear production games formulation is that the optimal solution obtained by solving OPTLP(S) may not be physically realizable, even when the federation S consists of only one cloud provider. We compared how far away the optimal feasible allocation for each cloud provider C_i to that of OPTLP({C_i}). This will also throw light when the federation S consists of more than one cloud provider.

We assume that the data centers owned by different cloud providers consist of physical machines with 96 cores, 200 GB RAM, and 2 TB secondary storage. This type of resource configuration is typical for server class machines. We computed the optimal feasible allocation for a cloud provider, DP({C_i}), using a dynamic programming approach. The average percentage over-estimation of revenue by using linear programming over dynamic programming is 19.8 percent. The cloud provider C₃ has the worst over-estimation error of 61.2 percent. This is due to the meager secondary storage availability when compared to cores and memory. Even cloud providers C₄,C₅ and C₉ have around 30 percent over-estimation error. This is due to the imbalance in the core and memory ratio. These atypical data center configurations are due to our randomization in the initial resource assignment to cloud providers in our experimental setup. Without these outliers, the average over-estimation error reduces to 10.5 percent.

Oligopolist price determination

In Intervention of an oligopolist in federation formation section, we studied how the price offer vector m=(m₁,⋯,m_n) made by an Oligopolist induces a stable coalition structure CS={F₁,⋯,F_k−1,F^∗}. The cloud providers in F^∗ would take up the price offer being made by the Oligopolist. Let us denote F^∗ as F^∗(m) to make its dependence on the price offer vector explicit.

Given a resource bundle b=(b^c,b^m,b^s), let U(b) denotes its utility for the oligopolist. If C(b) denotes the cost the oligopolist pays to acquire the resource bundle, then his profit P(b) is defined as follows.

$$ \begin{aligned} P(b) = U(b) - C(b) \end{aligned} $$

For example, with the price offer vector m, the resource bundle procured by the oligopolist is given by

$$ \begin{aligned} b(m)= \sum_{i\in F^{*}(m)} b_{i}. \end{aligned} $$

Then the profit made by him is given as follows.

$$ \begin{aligned} P(b(m))= U(b(m)) - \sum_{i\in F^{*}(m)} m_{i} \end{aligned} $$

The goal of the oligopolist is to come up with a price offer vector m such that P(b(m)) is maximized. Typically, an oligopolist has a higher utility for a resource bundle when compared with a cloud provider, due to the larger market reach and other value added services he can provide to the end users. So, it is safe to assume that for two resource vectors b₁ and b₂, if b₁≤b₂, then P(b₁)≤P(b₂). Hence, the oligopolist aims to acquire resources from all the cloud providers and while doing so he would like to minimize the total price offer he makes. In the next section, we show that if the oligopolist approaches the cloud providers in a sequential manner, one after another, then the total price offer he makes would be less than that of what he makes through a non-adaptive approach.

Non-adaptive vs adaptive price offer vectors

Non-adaptive pricing scheme

In the problem formulation from Intervention of an oligopolist in federation formation section, the oligopolist approaches all the cloud providers simultaneously with a price offer vector. Recall the cooperative linear production game G_lp=(N,v) from Federation formation and payoff distribution using linear production games section involving the cloud providers. The value of a cloud federation S⊆N, denoted by v(S), is obtained by solving the linear programming problem OPTLP(S). In particular, the value v(N) of the grand coalition is obtained by solving the linear programming problem OPTLP(N). The oligopolist can compute a core allocation α(N)=(α₁(N),⋯,α_n(N)) from the Owen set by solving the dual problem as discussed in Payoff distribution section. Then the oligopolist makes a price offer which is equal to that of core allocation α(N) and acquire all the resources from the cloud providers. Thus the total price offer he makes to acquire the maximal resource bundle b(N) is v(N).

Adaptive pricing scheme

Unlike the aforedescribed non-adaptive pricing scheme, it is possible for the oligopolist to approach one cloud provider at a time with a price offer possibly less than that of the pay-off he gets from core allocation, and thereby acquire the resource bundle b(N) at a total price less than v(N). The price offer vector in this case is denoted by an ordered n-tuple $\widetilde {m}=(\langle i_{1}, p_{1} \rangle, \cdots, \langle i_{n}, p_{n}\rangle)$. The n-tuple indicates that the cloud provider $C_{i_{1}}$ is approached first with a price offer p₁ and so on. We now define the optimal price offer vector $\widetilde {m}_{{opt}}(S)$ where S⊆N as follows.

Definition 10

For a coalition S⊆N, we say that a price offer vector $\widetilde {m}_{{opt}}(S)=(\langle i_{1}, p_{1} \rangle, \cdots, \langle i_{s}, p_{s}\rangle)$ made by an oligopolist is optimal if

• 1 All the cloud providers in S accept the offer.

• 2 $\sum _{i=1}^{s} p_{i}$ is minimal.

Let $\widetilde {v}_{{opt}}(S)=\sum _{i=1}^{s} p_{i}$ denote the optimal total price offer made by the oligopolist with respect to the coalition S. From Payoff distribution section, we know that we can compute the payoff distribution vector α(S)=(α₁(S),⋯,α_k(S)) for a coalition S⊆N by solving the dual of the problem OPTLP(S) and thereby obtain the shadow prices of the resources. Let Aut(S) denote the set of automorphisms or permutations of S. If the oligopolist approaches the cloud providers in an order determined by a permutation π∈Aut(S), then the total price offer made by him with respect to the permutation π, denoted as $\widetilde {v}_{\pi }(S)$, is given by the following recurrence relation.

$$ \begin{aligned} \widetilde{v}_{\pi}(S) = \alpha_{\pi(1)}(S) + \widetilde{v}_{\pi[2:s]}\left(S-\left\{\pi(1)\right\}\right) \end{aligned} $$

(4)

That is the oligopolist computes the payoff distribution vector for the coalition S. Then he buys out the cloud provider C_π(1) by making a price offer α_π(1)(S) which matches the payoff he obtains by remaining in the coalition. The same process is repeated by considering the reduced coalition S−{C_π(1)} and the permutation π[2:s](S−{C_π(1)}). This requires solving n OPTLP problems to compute $\widetilde {v}_{\pi }(N)$. The total optimal price offer is the minimum of price offers obtained by trying out all the permutations possible. It is given as follows.

$$ \begin{aligned} \widetilde{v}_{{opt}}(S) = \min_{\pi \in Aut(S)} \widetilde{v}_{\pi}(S) \end{aligned} $$

A simple brute force approach to computing $\widetilde {v}_{{opt}}(S)$ is by trying out all permutations. This requires solving n×n! OPTLP problems to compute $\widetilde {v}_{{opt}}(S)$. However, we can notice that there are only 2ⁿ distinct OPTLP problems corresponding to different subsets of N. Hence sub-problems repeat themselves and the redundant computations can be avoided by storing the solutions to all the sub-problems in a memoization table. This approach is similar to the one we adapt in dynamic programming algorithms. For example, consider the permutation π₁=(C₁,C₂,C₃,C₄,C₅) consisting of 5 cloud providers. After computing the price offer for C₁ and C₂ in two iterations, the oligopolist solves the subproblem with π₁[3:5]=(C₃,C₄,C₅) in (4). The same subproblem would be solved again for the permutation π₂=(C₂,C₁,C₃,C₄,C₅) after the payoff vectors for C₂ and C₁ are determined in that order. However, we can avoid the redundant computation by storing the solution to every newly solved subproblem and recalling it later whenever necessary. The following is a summary of the steps of the algorithm.

• 1 Precomputation Step Recall that α_i(S), for 1≤i≤n and S⊆N, denotes the payoff of the cloud provider C_i in the coalition S. Payoff distribution section shows how this value can be computed by solving the dual of OPTLP(S). We precompute these payoff values and store them in a table P by initializing the entries of the table as follows, P(C_i,S)=α_i(S).

• 2 Let M be the memoization table where M(S) stores the minimal total price offer the oligopolist makes to buy out all the cloud providers in the coalition S⊆N in an adaptive fashion. Each entry of this table is initialized to a very large value or it can be set to the value of the grand coalition v(N).

• 3 Let O be the memoization table where O(S) stores the order in which the oligopolist approaches the cloud providers to achieve the optimal price offer corresponding to M(S).

• 4 (i^th iteration) Compute M(S_i) where S_i⊆N is lexicographically the i^th subset.

  • (a) For each cloud provider C_j∈S_i:

    

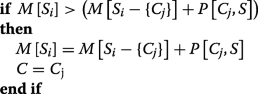
  • (b) O[S_i]=[C]+O[S_i−{C}]Extend the list

The time complexity of the above dynamic programming algorithm is Θ(n2ⁿ). This makes the algorithm practical to implement when compared with the naive algorithm with time complexity Θ(n!).

Consider the example from Experimental analysis section consisting of 12 cloud providers $\mathcal {I}=\{C_{1},\cdots, C_{12}\}$ whose resource capacities are given in Table 1. Further, various virtual machine types and their hourly rental costs are provided in Table 2. The value of the grand coalition $\mathcal {I}$ consisting of all the cloud providers is obtained by solving OPTLP($\mathcal {I}$). It is equal to $v(\mathcal {I})=77816$ when rounded to the nearest integer. This is the price at which the oligopolist can acquire the resources of all the cloud providers wherein he approaches them simultaneously i.e., in a non-adaptive fashion. The first row of the Table 3 in fact corresponds to a core allocation and gives the price offer made by the oligopolist to different cloud providers. The values in the Table 3 are rounded to the nearest integer for the sake of simplicity.

Table 3 In each iteration I_t, for 1≤t≤12, the oligopolist buys out a cloud provider by offering him a price which is equal to his payoff in the remnant grand coalition. This payoff to a cloud provider is suitably marked in each row of the table. The second column represents the remaining coalition members. The last column labeled $\widetilde {v}_{{opt}}$ represents the total price offer made by the oligopolist at the end of corresponding iteration. The last row gives the percentage loss of a cloud provider due to the adaptive strategy when compared with the payoff he gets from the non-adaptive strategy

In the adaptive approach, the oligopolist reaches out to different cloud providers one after another in such a way that the total price offer he makes is minimized. Using the proposed dynamic programming algorithm, we determined that [C₆,C₁₀,C₅,C₉,C₁₂,C₁₁,C₄,C₇,C₁,C₂,C₈,C₃] is the optimal order in which the oligopolist can approach the cloud providers. From Table 3, we can note that in Iteration 1, the oligopolist approaches cloud provider C₆ and makes a price offer 6078. This price offer is the same as what the cloud provider gets in the non-adaptive case. Hence he readily accepts, resulting in the new coalition $\mathcal {I}_{2} = [1-5,7-12]$. The oligopolist then obtains the core allocation for $\mathcal {I}_{2}$ by solving the dual of OPTLP($\mathcal {I}_{2}$). He then makes an offer of 10180 to cloud provider C₁₀ which is the payoff he obtains in the coalition $\mathcal {I}_{2}$. This leads to the coalition $\mathcal {I}_{3}=[1-5,7-9,11-12]$ for Iteration 3. The oligopolist repeats this process for 12 iterations. The cumulative price offer made by the oligopolist across iterations is given by the last column of the Table 3. The total adaptive price offer made by the oligopolist is 69459 which is 10.7 percent less than the total non-adaptive price offer. The last row of Table 3 shows the percentage loss of different cloud providers due to the adaptive approach when compared with the non-adaptive approach. We can notice that these percentages vary widely. For example, cloud provider C₆ faces no loss but cloud provider C₈ has a maximum loss percentage of 55.77. In general, the oligopolist pays the key cloud providers sufficiently and takes them out of coalition in the early iterations. This leaves the remnant coalition weak and thus the coalition members have to settle for a lesser price offer made by the oligopolist. Through this discussion we propose the following important theorem which we could not find in the prior literature to the best of our knowledge.

Theorem 3

In linear production games, the total adaptive price offer made by an oligopolist to buy out all the coalition members can be strictly less than the total non-adaptive price offer which is nothing but the value of the grand coalition.

The oligopolist can use a greedy approach instead of dynamic programming to find the order in which he can buy out the cloud providers. In the greedy approach, the oligopolist starts by making a price offer to the cloud provider with the least payoff in the grand coalition. In our example, it would be cloud provider C₄. This results in the new grand coalition N−C₄. The cloud provider computes the new payoff vector in the reduced grand coalition and again makes an offer to the cloud provider with the least payoff. This process is iterated until the oligopolist acquires the resources of all the cloud providers. In the example under consideration, the greedy approach yields the following order on the cloud providers [C₄,C₁,C₂,C₅,C₃,C₆,C₈,C₇,C₁₁,C₁₀,C₉,C₁₂], with a total price offer 77603, whereas the non-adaptive total price offer is 77816 and the dynamic programming based approach results in a total price offer of 69459.

Let DP_k denote the cloud providers acquired by the oligopolist using the optimal dynamic programming strategy. Let $P^{dp}_{k}$ denote the total payoff made by the oligopolist so far. Figure 5 compares the total payoff made by the oligopolist with the value v(DP_k) of the cloud providers if they form a coalition. This shows how the adaptive strategy is making gains with the progress in each iteration when compared with the non-adaptive strategy. Similarly, the line plots and depict the total payoff and coalition value at the end of each iteration. As can be observed that using the greedy strategy, the oligopolist does not gain any noticeable profit as the total payoff he makes is almost the same as the coalition value. However, in the case of dynamic programming approach, starting with iteration 9, the total price offer made by the oligopolist when compared with the coalition value starts going down. Finally, by the end of iteration 12, the total payoff made is 10.7 percent less than that of the coalition value, which directly turns into his profit. However, in the initial iterations, the dynamic programming approach seems to fare no better than the greedy approach as the oligopolist nets no profits.

Fig. 5

DP-CV plots the value of the coalition v(DP_k) and DP-TP plots the total payoff $P^{dp}_{k}$ made by the oligopolist. Analogous semantics hold for the GD-CV and GD-TP plots associated with the greedy strategy

Payoff analysis from random permutations

We recall from the previous section that the oligopolist makes a maximum and minimum total price offers of value 77816 and 69459. The maximum offer corresponds to the coalition value. The minimum offer is computed by using the dynamic programming algorithm, which gives us a strategic permutation to approach the cloud providers. We analyzed the total price offer distribution and the payoff distribution for each cloud provider by generating 10000 random permutations. Figure 6 shows the histogram of price offers made by the oligopolist. It can be noted that most of the total price offers are clustered around the maximum. In fact, we do not encounter any price offer close to the minimum, which is less than 70000. Table 4 shows the minimum, maximum, average, and standard deviation of the payoffs obtained by the individual cloud providers. We note that the variation in the oligopolist’s price offer is minor compared to the variation in each cloud provider’s payoff distribution. This could be because the oligopolist has to pay one cloud provider or other in the overall scheme of things. Thus his savings, although non-negligible but are meager.

Fig. 6

Histogram of total price offers made by the oligopolist from 10000 random permutations

Table 4 Payoff distribution for individual cloud providers based on 10000 random permutations

Related work

Grozev et al. [3] provided a systematic taxonomy of various inter-cloud architectures. The peer-to-peer inter-cloud architecture and the broker based multi-cloud architecture considered in this paper are based on their taxonomy. There has been several works on federation formation and payoff distribution using cooperative game theory [10–15]. However, none of these works consider the impact of an oligopolist or a monopolist on coalition formation which is the main focus of this paper. Niytao et al. [12] proposed the usage of stochastic linear programming games for payoff distribution among coalition members. The payoff distribution scheme we presented in this paper using linear production games is similar to their work. The closest work related to ours in literature is due to Fragnelli [16]. The author studied a market scenario which is very similar to that of ours but the specific problem addressed is the pricing strategy to be adopted by the players. Innes and Sexton [17] also studied very similar market scenario wherein the market unfolds in three stages. In Stage-1, the monopolist makes a price offer to the market players. Some of them may accept the offer and the rest reject. Those players who rejected form a coalition in Stage-2. Then the monopolist offers a price in Stage-3 to buy out the rest of the coalition. In our work, the monopolist approaches the cloud providers one after another in strategic fashion, thereby weakening the power of the remnant coalition continuously.

Conclusions

In this paper, we showed how we can model the influence of an oligopolist in a cloud market where multiple cloud providers can potentially come together to form a federation in order to increase their market reach. Further, we introduced the notion of stable coalition structures in the presence of oligopolists and a greedy algorithm for computing them. Next, we showed that by using a adaptive approach, wherein an oligopolist buys out cloud providers in a strategic order, he can do better than a non-adaptive approach, in terms of the total price offer he makes. We believe that our work paves way for further research in this less studied facet of federated cloud computing. Further, the proposed ideas are applicable to other markets beyond federated clouds.